Wasserstein GAN

Definition

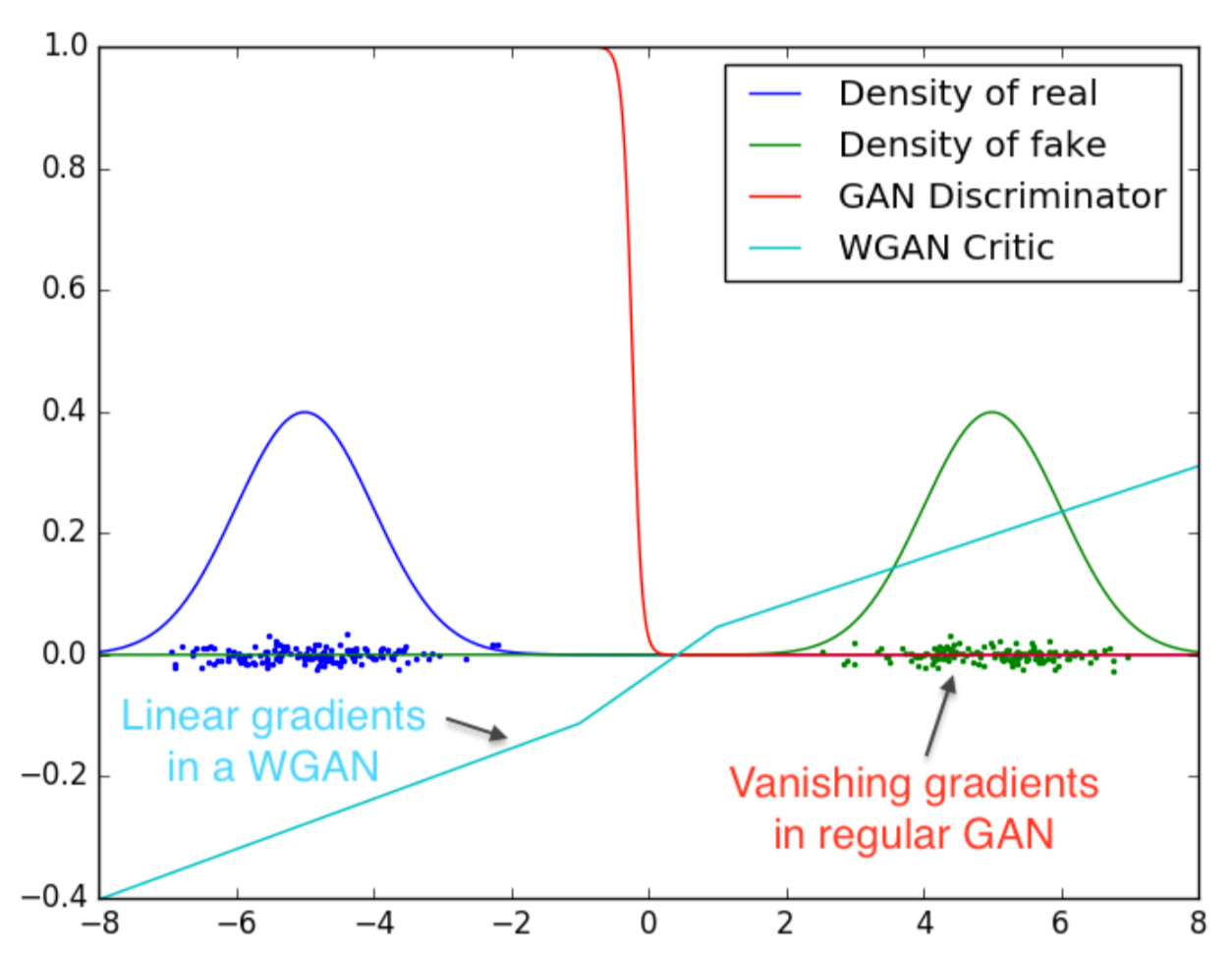
Wasserstein GAN (WGAN) is a variant of GAN that uses the Wasserstein Distance instead of the Jensen-Shannon Divergence used in traditional GAN. The Wasserstein distance provides a smoother gradient everywhere.

Architecture

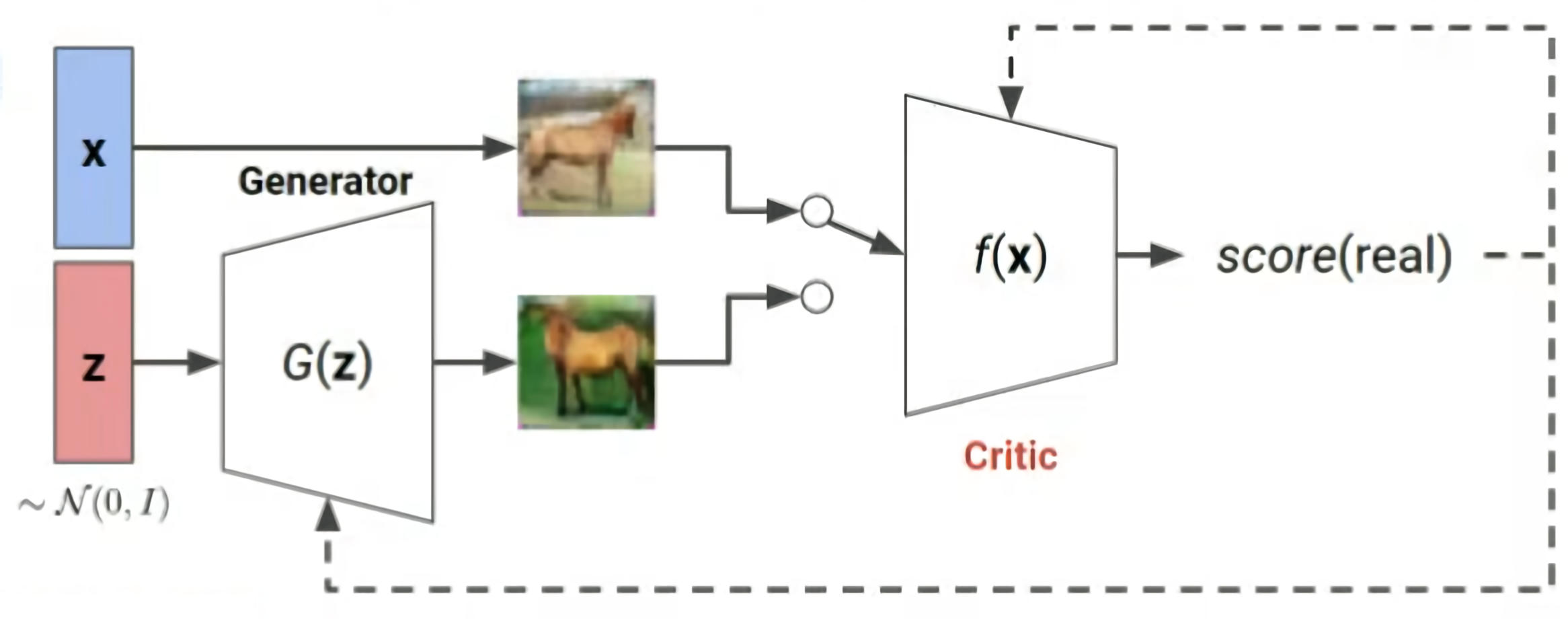
In WGAN, the discriminator of traditional GAN is replaced by a critic that is trained to approximate the Wasserstein Distance. The critic outputs a real number instead of a probability.

Since Wasserstein Distance is highly intractable, the cost function is simplified using Kantorovich-Rubenstein Duality requiring 1-Lipschitz continuous. To satisfy the condition the weights of the critic $f$ are clipped.

Objective Function

The objective function of WGAN is defined as ${\min }_{{\theta }_G}\underset{\approx W(P_r,p_z)}{\underbrace{\underset{{\theta }_f}{\max }[E_{x\sim p_r(x)}[f(x)]-E_{z\sim p_z(z)}[f(G(z))]]}}$ where:

• $G$ is the generator
• $f$ is the critic
• $p_r$ is the distribution of the input data
• $p_z$ is the distribution of noise

WGAN-GP

Instead of clipping the weights, WGAN-GP penalizes the model if the gradient norm moves away from its target norm value $1$.

The additional gradient penalty term of WGAN-GP $\lambda E_{x\sim p_x(x)}[(||{\nabla }_{{\theta }_f}f(x)|{|}_2-1{)}^2]$ where $f(x)=E_{x\sim p_r(x)}[f(x)]-E_{z\sim p_z(z)}[f(G(z))]$ is the critic loss.

This enforces the Lipschitz constraint more effectively than weight clipping.

Algorithm

$\alpha$: the learning rate, $c$: the clipping parameter, $m$: the batch size, $n_{\text{critic}}$: the number of iterations of the critic per generator iteration. ${\theta }_{f,0}$: the initial critic parameters. ${\theta }_{G,0}$: the initial generator’s parameters.

While $\theta$ has not converged:

1. for $t=0,\dots ,n_{\text{critic}}$:
   1. Sample $\{x^{(i)}{\}}_{i=1}^m\sim p_r(x)$ a batch from the real data.
   2. Sample $\{z^{(i)}{\}}_{i=1}^m\sim p_z(z)$ a batch from the noise distribution.
   3. $g_{{\theta }_f}={\nabla }_{{\theta }_f}\left[\frac{1}{m}\sum _{i=1}^{m}f(x^{(i)})-\frac{1}{m}\sum _{i=1}^{m}f(G(z^{(i)}))\right]$
   4. ${\theta }_{f,t+1}=w+\alpha \mathrm{RMSProp}({\theta }_{f,t},g_{{\theta }_f})$
   5. ${\theta }_{f,t+1}=\mathrm{clip}({\theta }_{f,t+1},-c,c)$
2. Sample $\{z^{(i)}{\}}_{i=1}^m\sim p_z(z)$
3. $g_{{\theta }_G}=-{\nabla }_{{\theta }_G}\frac{1}{m}\sum _{i=1}^{m}f(G(z^{(i)}))$
4. ${\theta }_{G,t+1}=\theta -\alpha \mathrm{RMSProp}(\theta ,g_{{\theta }_G})$