Definition
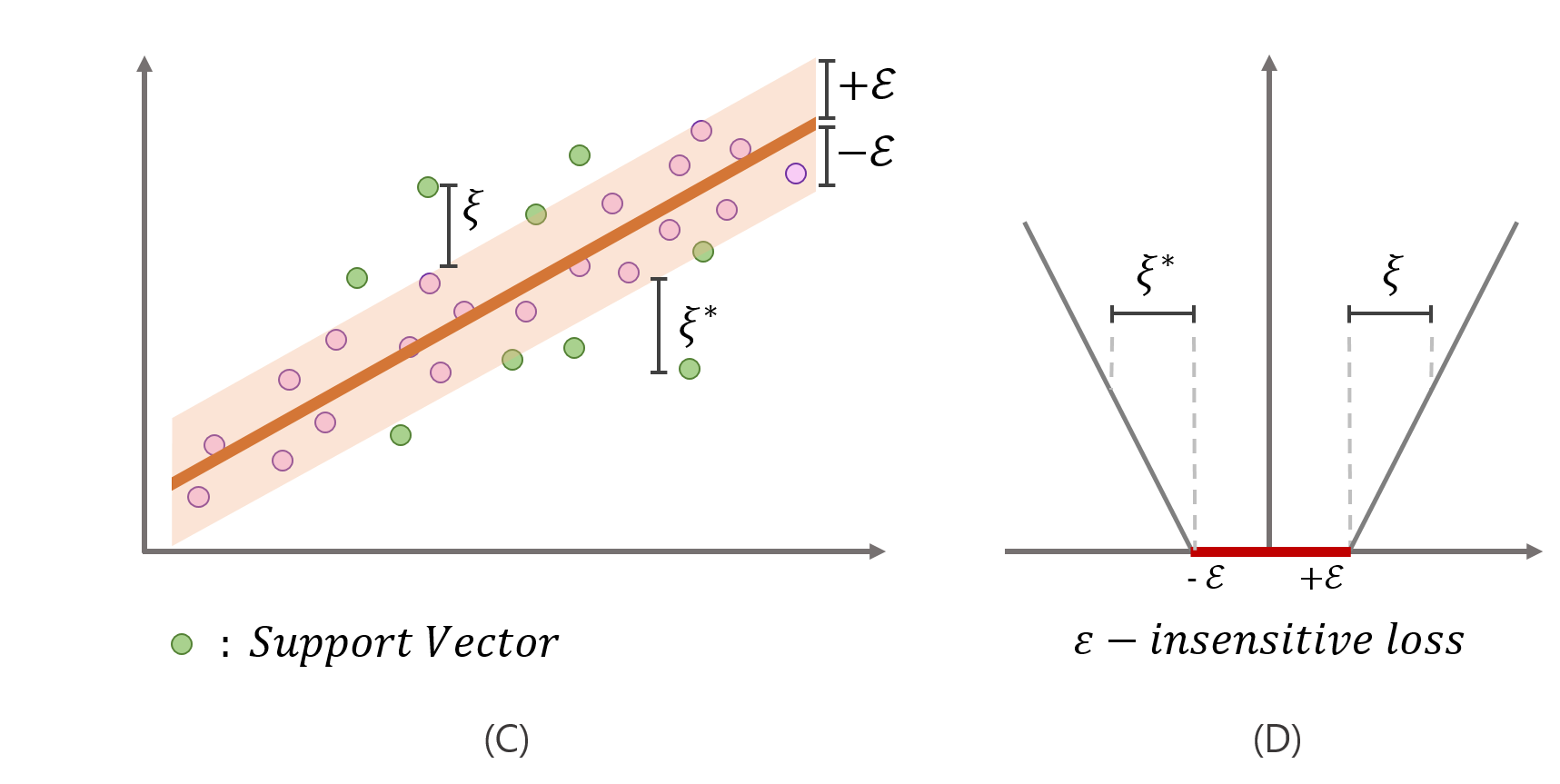
Support vector regression (SVR) depends only on a subset of the training data, because the loss function ignores any training data close to the model prediction, within a band or tube.
The primal optimization problem is defined as
\min &\left( \cfrac{1}{2}||\boldsymbol{\beta}||^{2} + C\sum\limits_{i=1}^{n}(\xi_{i} + \xi'_{i}) \right)\\ \text{subject to}\ &y_{i} - (\beta_{0} + \boldsymbol{\beta}^{\intercal}\mathbf{x}_{i}) \leq \epsilon + \xi'_{i},\\ &(\beta_{0} + \boldsymbol{\beta}^{\intercal}\mathbf{x}_{i}) - y_{i} \leq \epsilon + \xi_{i},\\ &\ \xi'_{i} \geq 0, \ \xi_{i} \geq 0\quad i=1,\dots,n \end{aligned}$$ The term $\cfrac{1}{2}||\boldsymbol{\beta}||^{2}$ in the objective function, which appears with the intention of maximizing the margin of SVM, acts as a regularization parameter in SVR. The Lagrangian primal function is defined as $$ \begin{aligned} L_{P} &= \frac{1}{2}||\boldsymbol{\beta}||^{2} + C\sum_{{i=1}}^{{n}} (\xi_{{i}} + \xi'_{{i}}) \\ &+ \sum_{{i=1}}^{{n}} \alpha'_{{i}} \left( y_{{i}} - (\beta_{0} + \boldsymbol{\beta}^{\intercal} \mathbf{x}_{{i}}) - \epsilon - \xi'_{{i}} \right) + \sum_{{i=1}}^{{n}} \alpha_{{i}} \left( (\beta_{0} + \boldsymbol{\beta}^{\intercal} \mathbf{x}_{{i}}) - y_{{i}} - \epsilon - \xi_{{i}} \right)\\ &- \sum_{{i=1}}^{{n}} \mu'_{{i}} \xi'_{{i}} - \sum_{{i=1}}^{{n}} \mu_{{i}} \xi_{{i}} \end{aligned} $$ with $\mathbb{\alpha}, \mathbb{\alpha}', \boldsymbol{\mu}, \boldsymbol{\mu}' \geq \mathbf{0}$ The dual optimization is defined as $$ \begin{aligned} \max\ &\left( \mathbf{y}^{\intercal} (\mathbf{\alpha} - \mathbf{\alpha'}) - \epsilon \mathbf{1}^{\intercal} (\mathbf{\alpha} + \mathbf{\alpha'}) - \frac{1}{2} (\mathbf{\alpha} - \mathbf{\alpha'})^{\intercal} \mathbf{K} (\mathbf{\alpha} - \mathbf{\alpha'}) \right) \\ \text{subject to}\ &\mathbf{1}_{n}^{\intercal} (\mathbf{\alpha} - \mathbf{\alpha'}) = 0, \mathbf{0} \leq \mathbf{a}, \mathbf{a}' \leq C\mathbf{1}_{n}\quad i=1,\dots,n \end{aligned}$$ And the dual Lagrangian function is defined as $$\begin{aligned} L_{D} = &\ \mathbf{y}^{\intercal} (\mathbf{\alpha} - \mathbf{\alpha'}) - \epsilon \mathbf{1}^{\intercal} (\mathbf{\alpha} + \mathbf{\alpha'}) - \frac{1}{2} (\mathbf{\alpha} - \mathbf{\alpha'})^{\intercal} \mathbf{K} (\mathbf{\alpha} - \mathbf{\alpha'}) \\ &+ \lambda \mathbf{1}_{n}^{\intercal} (\mathbf{\alpha} - \mathbf{\alpha'})\\ &- \boldsymbol{\mu}^{\intercal} \mathbf{\alpha} - \boldsymbol{\mu}'^{\intercal} \mathbf{\alpha'}+ \boldsymbol{\mu}_{C}^{\intercal} (C\mathbf{1}_{n} - \mathbf{\alpha}) + \boldsymbol{\mu}_{C}'^{\intercal} (C\mathbf{1}_{n} - \mathbf{\alpha'}) \end{aligned}$$ with $\boldsymbol{\mu}, \boldsymbol{\mu}', \boldsymbol{\mu}_{C}, \boldsymbol{\mu}_{C}' \geq \mathbf{0}$ where $\mathbf{K}$ is a [[Kernel Function]].