Life Table Estimator

Definition

Notations

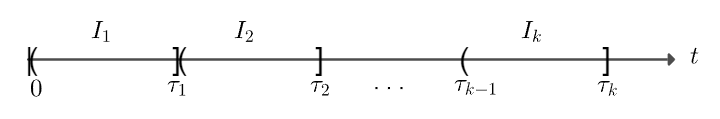
Assume intervals have equal length and let the notations:

• $I_i$: the $i$-th interval $({\tau }_{i-1},{\tau }_i]$ where ${\tau }_0=0$
• $n_i$: the number of individuals alive at the beginning of $I_i$
• $d_i$: the number of deaths during $I_i$
• $l_i$: the number of individuals censored during $I_i$
• $P_i$: $P(T>{\tau }_i|T>{\tau }_{i-1})=P(\text{surviving through}{I}_i|\text{alive at beginning of}{I}_i)$ where $T_i$ is the survival time.
• $q_i=1-P_i$

Estimation of Life Table Estimator

The life table estimator is derived from the expression $S(t)=\prod _{i=1}^k{P}_i$ where $P_i=P(T>{\tau }_i|T>{\tau }_{i-1})$

The life table estimator estimates the Survival Function as $\hat{S}({\tau }_k)=\prod _{i=1}^k{\hat{P}}_i$ where ${\hat{P}}_i=1-\frac{d_i}{n_i^{\prime }}$ and $n_i^{\prime }=n_i-\frac{l_i}{2}$ is called the effective sample size.

We assume that, on average, those individuals who became censored during $I_i$ were at risk for half the interval

Variance of Life Table Estimator

For a given $n_i^{\prime }$, assume that $n_i^{\prime }{\hat{P}}_i\approx B(n_i^{\prime },P_i)$, where $P_i=\frac{S({\tau }_i)}{S({\tau }_{i-1})}$. Since $\ln \hat{S}({\tau }_k)=\sum _{i=1}^k\ln {\hat{P}}_i$, under the assumption of the independence of $\ln {\hat{P}}_i$‘s, the variance of the life table estimator is approximated as $\mathrm{Var}[\ln \hat{S}({\tau }_k)]\approx \sum _{i=1}^k\mathrm{Var}[\ln {\hat{P}}_i]$ Then, by the Delta Method, Greenwood’s formula is derived as $\widehat{\mathrm{Var}}(\hat{S}({\tau }_k))=\hat{S}({\tau }_k{)}^2\sum _{i=1}^k\frac{d_i}{n_i^{\prime }(n_i^{\prime }-d_i)}$

Confidence Interval for Life Table Estimator

Under the asymptotic normality of the estimator, we can use $\hat{S}(t)\pm z_{\alpha /2}\sqrt{\widehat{\mathrm{Var}}(\hat{S}(t))}$ as a $100(1-\alpha )\%$ confidence interval for $S(t)$. However, this region could take values outside $(0,1)$. To avoid this kind of problem, the log-log-transformation is used.

Log-log Transformation

To guarantee for the CI of $S(t)$ to be within $(0,1)$, use log-log transformation. Let $V(t)=\ln (-\ln S(t))$. Then, by delta-method $\widehat{\mathrm{Var}}[\hat{V}(t)]\approx \frac{\widehat{\mathrm{Var}}(\hat{S}(t))}{[\ln \hat{S}(t){]}^2\hat{S}(t{)}^2}$ i.e. CI for $V(t)$ is $\hat{V}(t)\pm z_{\alpha /2}\sqrt{\widehat{\mathrm{Var}}(\hat{V}(t))}$ and CI for $S(t)$ is calculated as $\exp \left[-\exp \left(\hat{V}(t)\pm z_{\alpha /2}\sqrt{\widehat{\mathrm{Var}}(\hat{V}(t))}\right)\right]\in (0,1)$

Examples

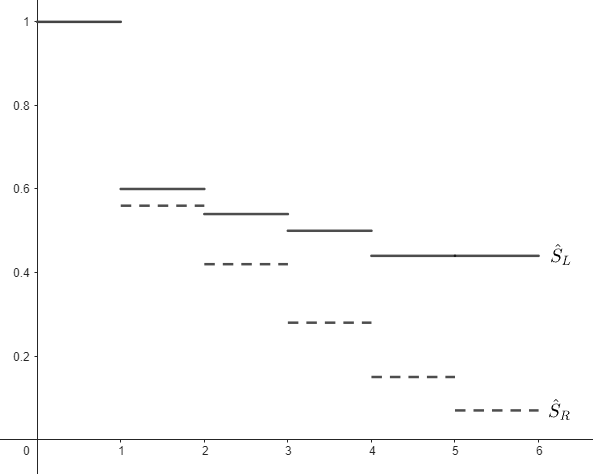
Consider a life table

$I_i$	$n_i$	$d_i$	$l_i$	$n_i^{\ast }=n_1-\sum _{j=1}^i{l}_j$	$d_i^{\ast }=\sum _{j=1}^i{d}_j$	${\hat{S}}_R=1-\frac{d_i^{\ast }}{n_i^{\ast }}$	$n_i^{\prime }=n_i-\frac{l_i}{2}$	${\hat{P}}_i=1-\frac{d_i}{n_i^{\prime }}$	${\hat{S}}_L=\prod _{j=1}^i{\hat{P}}_j$
$(0,1]$	$126$	$47$	$19$	$107$	$47$	$0.56$	$116.5$	$0.60$	$0.60$
$(1,2]$	$60$	$5$	$17$	$90$	$52$	$0.42$	$51.5$	$0.90$	$0.54$
$(2,3]$	$38$	$2$	$15$	$75$	$54$	$0.28$	$30.5$	$0.93$	$0.50$
$(3,4]$	$21$	$2$	$9$	$66$	$56$	$0.15$	$16.5$	$0.88$	$0.44$
$(4,5]$	$10$	$0$	$6$	$60$	$56$	$0.07$	$7$	$1.00$	$0.44$
where ${\hat{S}}_R$ is the Reduced Sample Estimator and ${\hat{S}}_R$ is the life table estimator.

The survival functions are estimated as