Graph Isomorphism Network

Definition

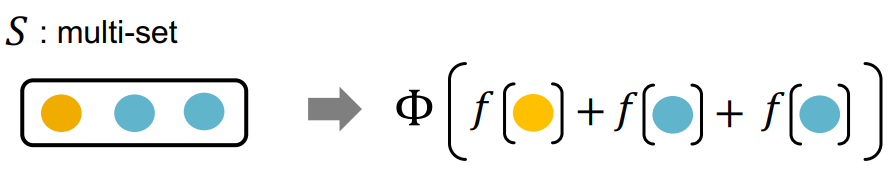
The Graph isomorphism network (GIN) is a GNN architecture having better expressive power and ability to distinguish different graph structures with injective aggregation.

Architecture

GNNs generates a Node Embedding using the computational graph corresponding to a subtree rooted around each node. The most expressive GNN maps different computational graphs (rooted subtrees) into different node embeddings. If each step of GNN’s neighbor aggregation is injective, then the model retains the full neighboring information. So, the generated node embeddings can distinguish different rooted subtrees.

Any injective multi-set function can be expressed as $\varphi \left(\sum _{x\in S}f(x)\right)$ where the functions $\Phi$ and $f$ are both some non-linear functions.

Thanks to the Universal Approximation Theorem it can be approximated with multi-layer perceptrons. ${\mathrm{MLP}}_{\varphi }\left(\sum _{x\in S}{\mathrm{MLP}}_f(x)\right)$

GIN uses the injective aggregation with the features of a node and its neighbors.

h_{i}^{(k)} &= \operatorname{MLP}_{\phi}^{(k)}\left((1+\epsilon^{(k)})\operatorname{MLP}^{(k)}_{f}(h_{i}^{(k-1)})+ \sum\limits_{j \in \mathcal{N}(v_{i})}\operatorname{MLP}^{(k)}_{f}(h_{j}^{(k-1)}) \right)\\ &\approx \operatorname{MLP}^{(k)}\left((1+\epsilon^{(k)})h_{i}^{(k-1)} + \sum\limits_{j \in \mathcal{N}(v_{i})} h_{j}^{(k-1)}\right) \end{aligned}$$ where $\epsilon^{k}$ is a learnable scalar ensuring the central node's features.