Constrained Extremum Theorem

Definition

Let the eigenvalues of $n\times n$ matrix $A$ be ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$ and corresponding eigenvalues be ${\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_n$. Then, satisfies following properties

• $\exists$ the minimum and maximum of Quadratic Form ${\mathbf{v}}^{⊺}\mathbf{Av}$ on the unit circle $||\mathbf{v}||=1$
• $\exists$ the maximum of $\mathbf{A}$, as the largest eigenvalue ${\lambda }_1$ at the point of the corresponding eigenvector ${\mathbf{v}}_1$
• $\exists$ the minimum of $\mathbf{A}$, as the smallest eigenvalue ${\lambda }_n$ at the point of the corresponding eigenvector ${\mathbf{v}}_n$ where the condition $||\mathbf{v}||$ is called the constraint and the minimum and maximum are called the constrained extreme

Examples

$||\mathbf{v}||=1\iff \sqrt{x^2+y^2}=1$

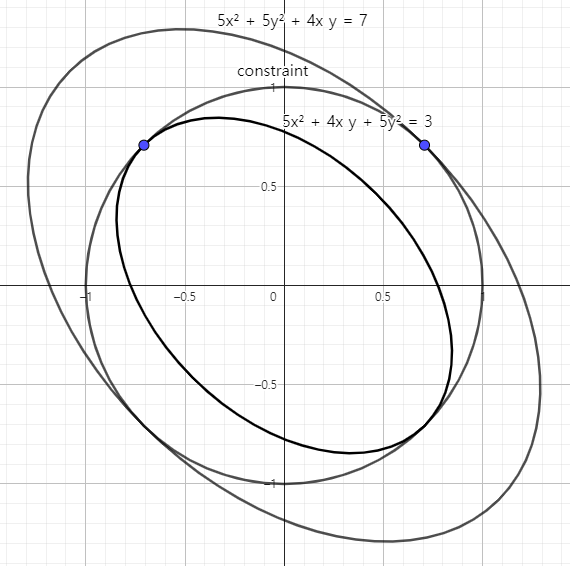
Let the square equation be $z=5x^2+5y^2+4xy$ Then the quadratic form be $z=\left[\begin{array}{cc}x& y\end{array}\right]\left[\begin{array}{cc}5& 2\\ 2& 5\end{array}\right]=\left[\begin{array}{c}x\\ y\end{array}\right]$ The eigenvalues are ${\lambda }_1=7,{\lambda }_2=3$ and the corresponding eigenvectors are ${\mathbf{v}}_1=(1,1),{\mathbf{v}}_2=(-1,1)$ $\therefore z$ has the maximum value $7$ at $(x,y)=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$ and has the minimum value $3$ at $(x,y)=(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$