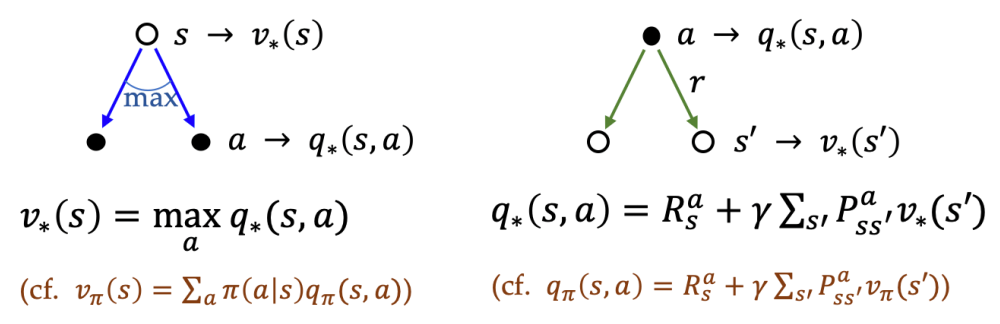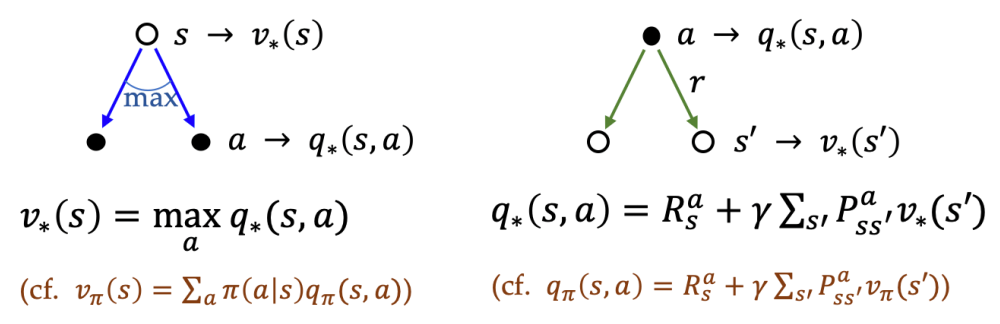Definition
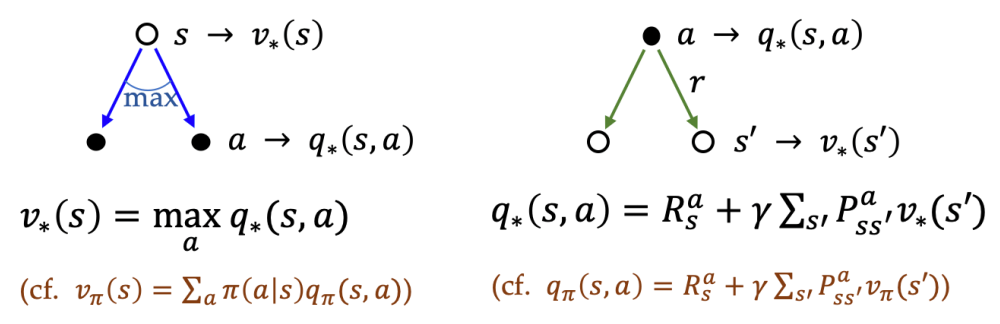
Under model-based (known MDP), the optimal value functions can be iteratively evaluated by dynamic programming.
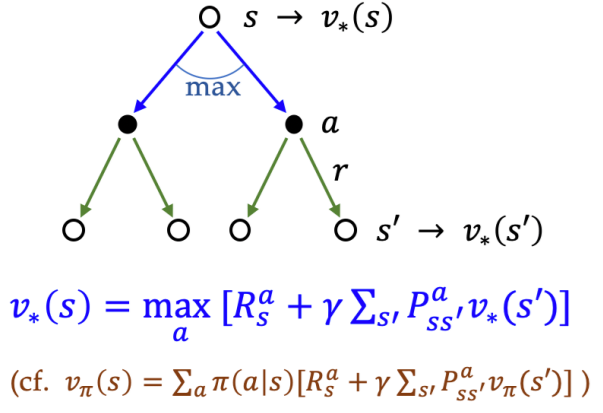
v_{*}(s)
&= \max_{a} q_{*}(s, a)\\
&= \max_{a} E_{\pi_{*}}[G_{t} | S_{t}=s, A_{t}=a]\\
&= \max_{a} E_{\pi_{*}}[R_{t+1} + \gamma G_{t+1} | S_{t}=s, A_{t}=a]\\
&= \max_{a} E_{s',r}[R_{t+1} + \gamma v_{*}(S_{t+1}) | S_{t}=s, A_{t}=a]\\
&= \max_{a} \sum\limits_{s',r}p(s', r | s, a) [r + \gamma v_{*}(s')]\quad \left( =\max_{a} [R_{s}^{a} + \gamma\sum\limits_{s'}P_{ss'}^{a} v_{*}(s')] \right)
\end{aligned}$$
## Bellman Optimality Equation for [[Action-Value Function]]
![[Pasted image 20241207152144.png|450]]
$$\begin{aligned}
q_{*}(s, a)
&= E_{s',r}[R_{t+1} + \gamma \max_{a'} q_{*}(S_{t+1}, a') | S_{t}=s, A_{t}=a]\\
&= \sum\limits_{s',r}p(s',r | s, a)[r + \gamma \max_{a'} q_{*}(s', a')]\quad \left(= R_{s}^{a} + \gamma \sum\limits_{s'}P_{ss'}^{a} \max_{a'} q_{*}(s', a') \right)
\end{aligned}$$