Barrier Method

Definition

An interior point optimization technique used to solve constrained optimization problems. It involves adding a barrier or penalty term to the objective function that penalizes solutions for being outside the feasible region.

Algorithm

Consider the optimization problem with an inequality constraint

$\underset{x}{\min }f(x)$ subject to $g(x)\le 0,h(x)=0$

The KKT Conditions of the problem are the following

• $\nabla f(x)+\lambda \nabla h(x)+\mu \nabla g(x)=0$^[Stationarity]
• $h(x)=0,g(x)\le 0$^[Primal feasibility]
• $\mu \ge 0$^[Dual feasibility]
• $\mu g(x)=0$^[Complementary slackness]

Interior point methods solve the problem whose complementary slackness condition is relaxed $\mu g(x)=-t$ where $t>0$ $\Rightarrow \mu =-\frac{t}{g(x)}$

the stationary condition become $\nabla f(x)+\lambda \nabla h(x)-t\frac{\nabla g(x)}{g(x)}=0\iff \nabla f(x)+\lambda \nabla h(x)-t\ln (-g(x))=0$ where $-t\ln (-g(x))$ is called a logarithmic barrier function

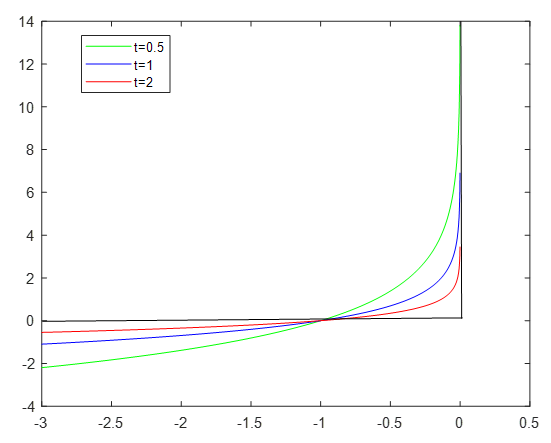As $t$ large, the logarithmic barrier function functions like an indicator function.

Now, by the definition of log function, $g(x)$ should be negative or zero, so the primal feasibility condition holds. Also, by the relaxed complementary slackness conditions, $\mu$ is positive or zero, so the dual feasibility conditions holds

Now the conditions have to be satisfied are the following

• $\nabla f(x)+\lambda \nabla h(x)-t\nabla \ln (-g(x))=0$
• $h(x)=0$
• $-g(x)>0$
• $t>0$

and the problem with inequality become the problem with equality $\underset{x}{\min }f(x)-t\ln (-g(x))$ subject to $h(x)=0$

It can be solved using Newton’s Method

Newton’s Method’s approximation becomes unstable if $t$ is too small and the current point is far from optimal. So, we initially choose large $t$ and iteratively shrink it.

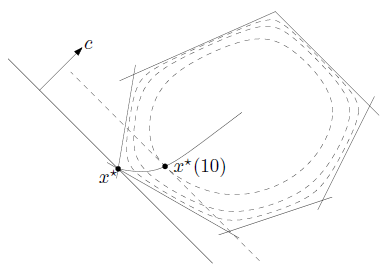
Analytic Central Point of Feasible Region

If $t$ is very large, then the optimization problem become the following. $\underset{x}{\min }-t\ln (-g(x))$ subject to $h(x)=0$

Since $\ln$ is a monotonic increasing function, the problem can be transformed as $\underset{x}{\min }g(x)$ subject to $h(x)=0$

So, it finds the analytic central point of feasible region (gravity of the feasible region)

Phase 1 method

In the iteration, we have to find the initial points satisfying constraints $t_0,x_{0,}{\lambda }_0$ satisfying $t_0>0,g(x_0)<0$

To ensure the $g(x_0)<0$ condition, transform the optimization problem only at the initial stage. $\underset{x}{\min }f(x)-t_0\ln (s-g(x))$ subject to $h(x)=0,s=0$

Now the problem can be solved using Infeasible Start Newton’s Method