Orientability

Definition

A surface is orientable if a normal vector can be consistently defined at every point of the surface. In other words, a coherent notation of up and down or inside and outside can be assigned across the entire surface. If a surface is not orientable, it is a non-orientable surface.

Examples

Genera	$0$	$1$	$2$	$\dots$	$n$
Orientable	$S^2$ Sphere	$T^2$ Torus	$T^2\#T^2$ Double torus	$\dots$	$\stackrel{n}{\#}{T}^2$ genus-n torus
Non-orientable		$P^2=S^2/(x\sim -x)$ Cross surface (Projective plane)	$KB\cong P^2\#P^2$ Klein bottle	$\dots$	$\stackrel{n}{\#}{P}^2$ n-times connected projective plane
where $\#$ is a Connected Sum operator.

Orientable Surfaces

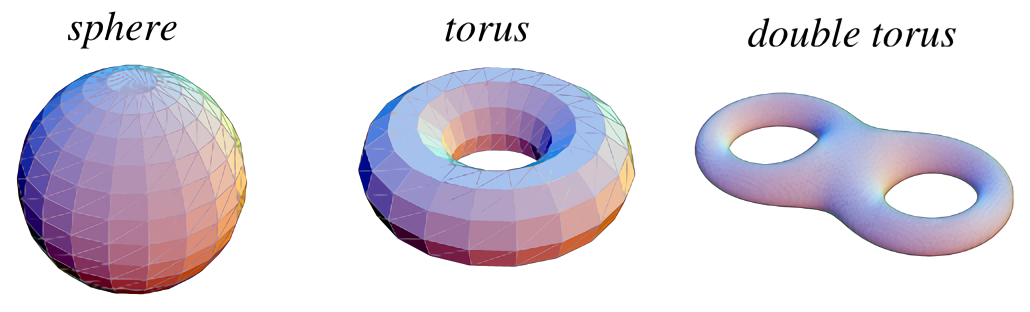
Non-Orientable Surfaces

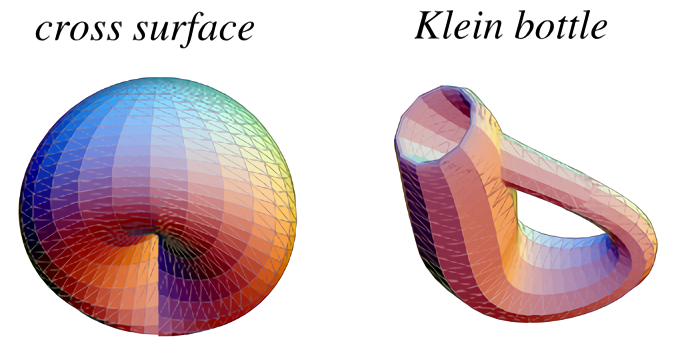
Facts

Non-orientable surfaces contain Mobius bands.

A surface can be classified by its number of genera and orientability.