Definition
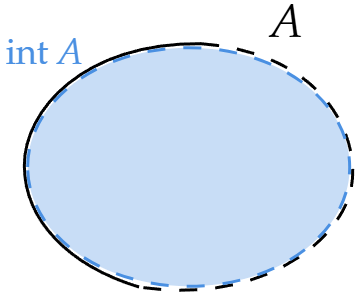
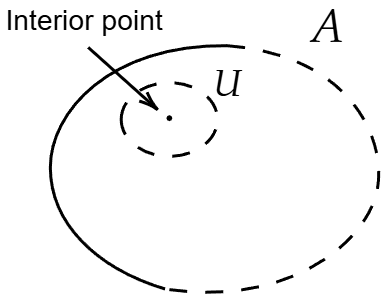
Consider a subset of a Topological Space . The interior of is defined as
\mathring{A} = \operatorname{int}A &:= \{ x \in X | \exists U \in \mathcal{T}\ \text{s.t.}\ x\in U \subset A \} \\ &= \bigcup \{ U | U \in \mathcal{T}\ \text{and}\ U \subset A \} \\ \end{aligned}$$ The interior of the $A$ can be defined in any of the following equivalent ways: - $\operatorname{int}A$ is the set of all interior points of $A$ - $\operatorname{int}A$ is the largest open subset of $X$ contained in $A$ - $\operatorname{int}A$ is the union of all open sets of $X$ contained in $A$ ## Definition for Metric Space $$\mathring{A} = \operatorname{int}A = \{x | \exists\epsilon>0, B(x, \epsilon) \subset A\}$$ where $B(x, \epsilon)$ is an open ball with a center $x$ and radius $\epsilon$. # Facts > For subsets $A, B$ of a [[Topological Space]] $(X, \mathcal{T})$, > $$A \subset B \Longrightarrow \operatorname{int} A \subset \operatorname{int} B$$ > For subsets $A, B$ of a [[Topological Space]] $(X, \mathcal{T})$, > $$\operatorname{int}(A \cap B) = \operatorname{int} A \cap \operatorname{int} B$$