Gaussian Process Regression

Definition

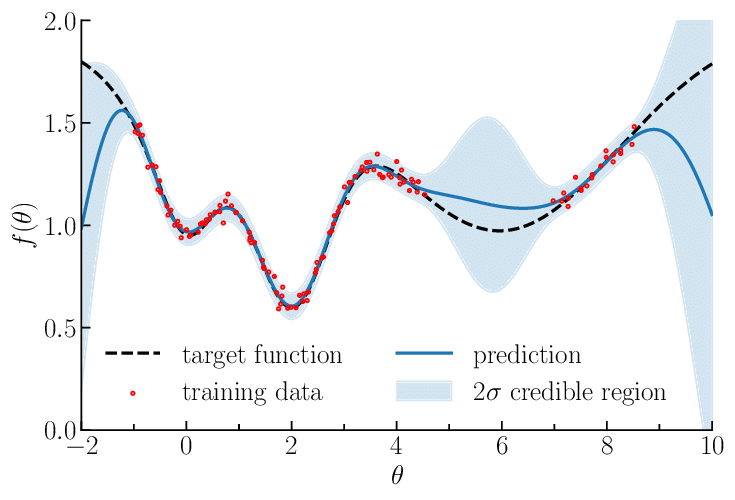
Gaussian Process Regression (GPR) is a non-parametric Bayesian approach to regression provides uncertainty estimates in addition to point estimates. GPR assumes that the values of the function at different points are jointly Gaussian distributed.

Consider a training dataset $\mathcal{D}=\{({\mathbf{x}}_i,y_i){\}}_{i=1}^N$, and a test points $\{{\mathbf{x}}_i^{\ast }{\}}_{i=1}^M$ (Assume the $y_i$‘s have $0$ mean). The task of GPR is providing predictive distributions on the test points.

The model assume that the observed target values $y_i$ are noisy version of the underlying true function $f({\mathbf{x}}_i)$. $y_i=f({\mathbf{x}}_i)+{ϵ}_i$ where ${ϵ}_i\sim N(0,{\sigma }_{ϵ}^2)$ is Gaussian noise with variance ${\sigma }_{ϵ}^2$.

By The Gaussian process assumption, the observations $\mathbf{y}$ and the true function outputs ${\mathbf{f}}^{\ast }$ at given test points ${\mathbf{X}}^{\ast }$ are jointly distributed as an $(N+M)$-dimensional Multivariate Normal Distribution specified by Kernel Function $\mathcal{K}$.

$$N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}{\hat{\mathbf{K}}}_{\mathbf{X},\mathbf{X}}& {\mathbf{K}}_{\mathbf{X},{\mathbf{X}}^{\ast }}\\ {\mathbf{K}}_{{\mathbf{X}}^{\ast },\mathbf{X}}& {\mathbf{K}}_{{\mathbf{X}}^{\ast },{\mathbf{X}}^{\ast }}\end{array}\right]\right)$$

Where:

• ${\mathbf{K}}_{\mathbf{X},\mathbf{X}}$ is the covariance matrix of all similarities $[{\mathbf{K}}_{\mathbf{X},\mathbf{X}}{]}_{ij}=\mathcal{K}({\mathbf{x}}_i,{\mathbf{x}}_j)$ where $\mathcal{K}$ is a kernel function.
• ${\hat{\mathbf{K}}}_{\mathbf{X},\mathbf{X}}={\mathbf{K}}_{\mathbf{X},\mathbf{X}}+{\sigma }_{ϵ}^2{\mathbf{I}}_N$

The posterior distribution over ${\mathbf{f}}^{\ast }$ comes from conditioning ${\mathbf{f}}^{\ast }|{\mathbf{X}}^{\ast },\mathcal{D}\sim N({\mu }_{{\mathbf{f}}^{\ast }},{\Sigma }_{{\mathbf{f}}^{\ast }})$ Where:

• ${\mu }_{{\mathbf{f}}^{\ast }}={\mathbf{K}}_{{\mathbf{X}}^{\ast },\mathbf{X}}{\hat{\mathbf{K}}}_{\mathbf{X},\mathbf{X}}^{-1}\mathbf{y}$
• ${\Sigma }_{{\mathbf{f}}^{\ast }}={\mathbf{K}}_{{\mathbf{X}}^{\ast },{\mathbf{X}}^{\ast }}-{\mathbf{K}}_{{\mathbf{X}}^{\ast },\mathbf{X}}{\hat{\mathbf{K}}}_{\mathbf{X},\mathbf{X}}^{-1}\mathbf{y}{\mathbf{K}}_{\mathbf{X},{\mathbf{X}}^{\ast }}$

The predictive mean ${\mu }_{{\mathbf{f}}^{\ast }}$ gives the expected function values at the test points, and the predictive covariance matrix ${\Sigma }_{{\mathbf{f}}^{\ast }}$ quantifies the uncertainty in the predictions.

The computational complexity of GPR is $O(n^3)$ due to the matrix inversion required for calculating the posterior, making it less suitable for large datasets.

Kernel Function

The kernel function $\mathcal{K}(\mathbf{x},{\mathbf{x}}^{\prime })$ measures the similarity or correlation between two inputs $\mathbf{x}$ and ${\mathbf{x}}^{\prime }$. The choice of the kernel function is crucial as it encodes prior assumptions about the properties of the function, such as smoothness and periodicity.

Examples

• RBF kernel assumes that nearby points are highly correlated, resulting in smooth function estimates. $\mathcal{K}(\mathbf{x},{\mathbf{x}}^{\prime })=\exp \left(-\frac{\Vert \mathbf{x}-{\mathbf{x}}^{\prime }{\Vert }^2}{2l^2}\right)$
• Periodic (Exp-Sine-squared) Kernel: $\mathcal{K}(\mathbf{x},{\mathbf{x}}^{\prime })=\exp \left(-\frac{2}{l^2}{\sin }^2(\frac{\pi }{p}\Vert \mathbf{x}-{\mathbf{x}}^{\prime }\Vert )\right)$
• Linear (Dot-product) kernel models linear relationships between inputs and outputs $\mathcal{K}(\mathbf{x},{\mathbf{x}}^{\prime })={\sigma }_0^2+\mathbf{x}\cdot {\mathbf{x}}^{\prime }$

Kernels can also be combined (e.g., by addition or multiplication) to create more complex and flexible covariance structures.