Existence and Uniqueness Theorem

Definition

First-order

Let $f:(x,y)\to \mathbb{R}$ be a continuous as a function of $x,y$ and lipschitz continuous in $y$. Then, $y^{\prime }=f(x,y),y(x_0)=y_0$ has a unique solution $y$

Thm 2.4.1

$p(t),g(t)$ are continuous on an open interval $I=(\alpha ,\beta ),t_0\in I,y_0\in \mathbb{R}$

$\Rightarrow$ There exist a unique function $y=\varphi (t)$ satisfying a linear ODE $y^{\prime }=p(t)y=g(t)$
for each $t\in I$ and satisfying the initial condition $y(t_0)=y_0$

Thm 2.4.2

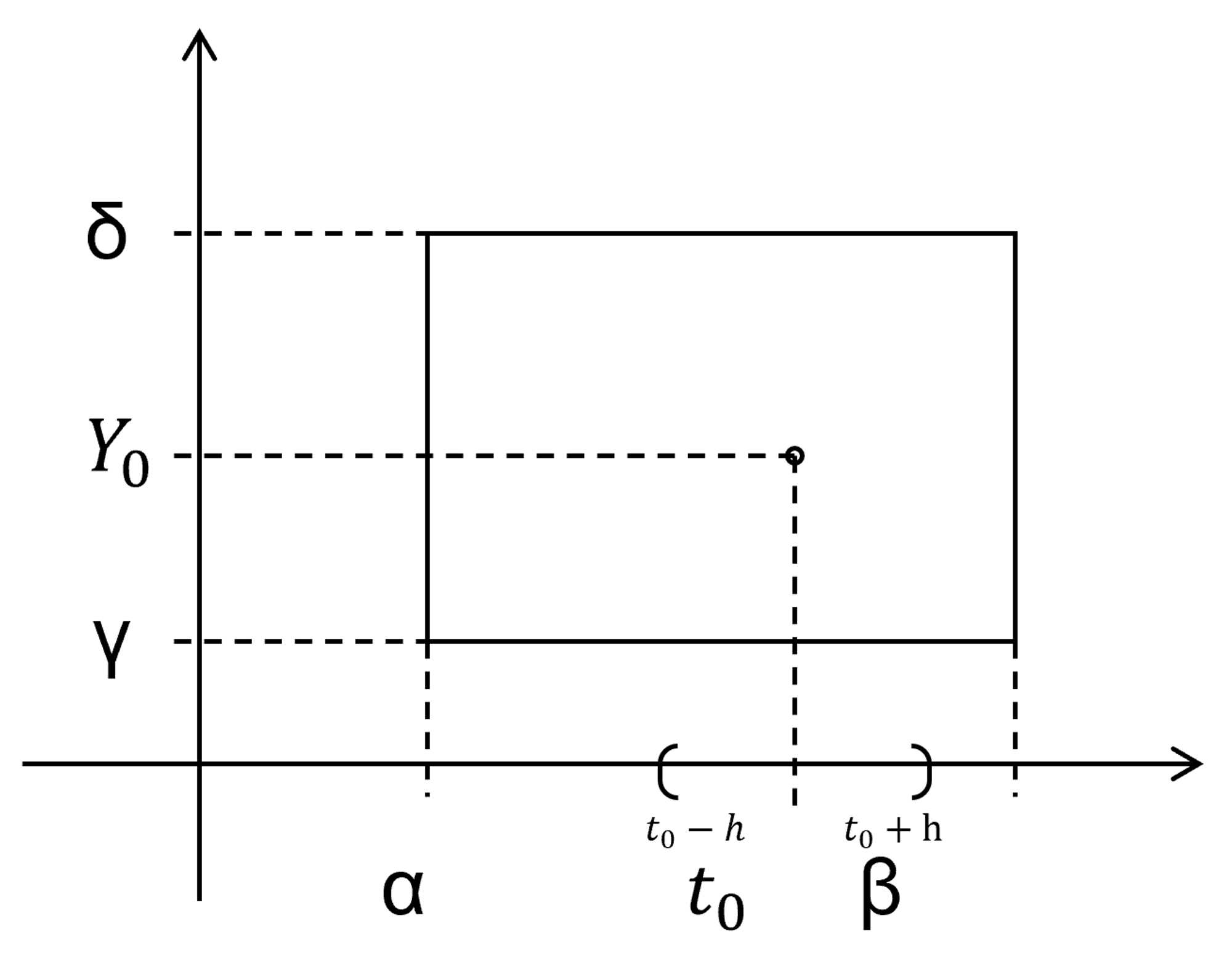Consider an I.V.P $y^{\prime }=f(t,y),y(t_0)=y_0$

$f$ and $\frac{\partial f}{\partial d}$ are continuous in $R=\{(x,y)|\alpha <t<\beta ,\gamma <y<\delta \}$ and $(t_0,y_0)\in \mathbb{R}$

$\Rightarrow$ There exists $h>0$ s.t. $(t_0-h,t_0+R)\subset (\alpha ,\beta )$
and a unique solution $y=\varphi (t)$ defined on $(t_0-h,t_0+h)$ of the I.V.P

${\varphi }^{\prime }(t)=f(y,\varphi (t))\forall t\in (y_0-h,t_0+h)$ and $\varphi (t_0)=y_0$

If ODE is linear, $f(t,y)=-p(t)y+g(t)$, so $f=-py+g,\frac{\partial f}{\partial y}=-p$ both are continuous.
(condition of Thm 2.4.2 $\iff$ condition of Thm 2.4.1)

Thm 2.4.2 guarantee the existence of a unique solution of I.V.P in $(t_0-h,t_0+h)$ not in $(\alpha ,\beta )$

Second-order

Thm 1 (Existence and Uniqueness Theorem for I.V.P)

Let $p(t),g(t),r(t)$ be continuous on some open interval $I=(\alpha ,\beta )$

If $L(y)=y^{\prime \prime }+p{y}^{\prime }+qy=r,y(t_0)=k_0,y^{\prime }(t_0)=k_1$ for some $t_0\in I$ then, this I.V.P has a unique solution $y=\varphi (t)$ on $I$

Thm 2 (Linear Independence / Dependence of Solutions)

Let $p,q$ be continuous on $I$ and $y_1,y_2$ be solutions of $L(y)=y^{\prime \prime }+p{y}^{\prime }+qy=0$. Then,

$y_1,y_2$ are linearly independent $\iff W(y_1,y_2)(t)\ne 0\text{for all}t\in I$ $\iff W(y_1,y_2)(t)\ne 0\text{for some}t\in I$

$y_1,y_2$ are linearly dependent $\iff W(y_1,y_2)(t)=0\text{for all}t\in I$ $\iff W(y_1,y_2)(t)=0\text{for some}t\in I$

where $W$ is Wronskian Determinant

Thm 3 (Existence of a general solution)

Let $p,q$ be continuous on an open interval $I=(\alpha ,\beta )$

Then, the ODE $y^{\prime \prime }+p{y}^{\prime }+qy=0$ has a general solution

Thm 4 (General solutions includes all solutions)

Let $p,q$ be continuous on an open interval $I=(\alpha ,\beta )$

Let $y_1,y_2$ be a basis of the solutions of the ODE $y^{\prime \prime }+p{y}^{\prime }+qy=0$ on $I$

Then every solution $y=Y(t)$ of $y^{\prime \prime }+p{y}^{\prime }+qy=0$ on $I$ is of the form $Y(x)=c_1{y}_1+c_2+y_2$ for some $c_1,c_2\in \mathbb{R}$

Higher-order ODE

Thm 4.1.1 (Existence and uniqueness)

Let $L(y)=\underset{=\sum _{k=0}^n{p}_k(x)y^{(k)},p_n(x)=1}{\underbrace{y^{(n)}+p_{n-1}(x)y^{(n-1)}+\cdots +p_1(x)y^{\prime }+p_0(x)y}}=r(x)⊛$ be an n-th order linear ODE

Then, I.V.P $(⊛,y(x_0)=k_0,y^{\prime }(x_0)=k_1,\dots ,y^{(n-1)}(x_0)=k_{n-1})$ has a unique solution on $I$

Thm 4.1.2 & 4.1.3

When $p_0,p_1,\dots ,p_{n-1}$ continuous on $I$, let $y_1,\dots y_n$ be solution of $⊛$. Then,

$W(y_1,\dots y_n)(x_0)\ne 0$ for some $x_0\in I$ $\iff (y_1,\dots y_n)(x)\ne 0$ for all $x\in I$ $\iff y_1,\dots y_n$ are linearly independent

Also, equivalently,

$W(y_1,\dots y_n)(x_0)=0$ on $I$ $\iff (y_1,\dots y_n)(x)=0$ for some $I$ $\iff y_1,\dots y_n$ are linearly dependent